SOAL DAN PEMBAHASAN FUNGSI TRIGONOMETRI

 

SOAL DAN PEMBAHASAN FUNGSI TRIGONOMETRI

Nama: Arini Fitria Afrizal(03)

kelas: X MIPA 1

1. Perhatikan gambar berikut!

Gambar di atas mempunyai persamaan ...

a. y = cos x

b. y = 3 cos x

c. y = cos 3x

d. y = 3 sin x

e. y = sin 3x

Jawab:

Grafik di atas adalah grafik cosinus.

Bentuk umum fungsinya adalah y = k . cos a (x ± α)

k = 3

Maka persamaan yang memenuhi grafik di atas adalah y = 3 cos x

Jawaban yang tepat B.

2. perhatikan grafik berikut!

Persamaan dari grafik di atas adalah...

a. y = -sin x

b. y = -cos x

c. y = 1 – cos x

d. y = sin x + 1

e. y = -sinx – 1

Jawab:

Grafik di atas adalah grafik sinus.

Bentuk umum fungsinya adalah y = k . sin a (x ± α)

k = -1

Maka persamaan yang memenuhi grafik di atas adalah y = -sin x

Jawaban yang tepat A.

3. Nilai maksimum dari fungsi y = 2 sin (x + 60⁰) + 1 adalah...

a. 3

b. 2

c. 0

d. -2

e. -1

Jawab:

y = 2 sin (x + 60⁰) + 1

y = 2 (1) + 1 = 3 (nilai maksimum)

y = 2 (-1) + 1 = -1 (nilai minimum)

Jawaban yang tepat A.

4. Nilai minimum dari fungsi y = -2 cos 3/2 x adalah...

a. -2

b. -1

c. 0

d. 1

e. 2

Jawab:

y = -2 cos 3/2 x

y = -2 (1) = -2 (nilai minimum)

y = -2 (-1) = 2 (nilai maksimum)

Jawaban yang tepat A.

5. Nilai maksimum dari fungsi y = sin x – 1 adalah...

a. 0

b. 1

c. 2

d. -2

e. -1

Jawab:

y = sin x – 1

y = 1 – 1 = 0 (nilai maksimum)

y = -1 – 1 = -2 (nilai minimum)

Jawaban yang tepat A.

6. Perhatikan grafik berikut!

Persamaan grafik di atas adalah...

a. y = 2 cos (x + 90⁰)

b. y = 2 cos (x + 180⁰)

c. y = 2 sin ( x + 90⁰)

d. y = sin (x + 180⁰)

e. y = cos (x – 90⁰)

Jawab:

Grafik di atas adalah grafik cosinus.

Bentuk umum fungsinya adalah y = k . cos a (x ± α)

k = 2

Maka persamaan yang memenuhi grafik di atas adalah y = 2 cos (x + 180⁰)

Jawaban yang tepat B.

7. Nilai minimum dari y = ½ cos x adalah...

a. -1

b. – ½ 

c. 0

d. ½ 

e. 1

Jawab:

y = ½ cos x

y = ½ (1) = ½ (nilai maksimum)

y = ½ (-1) = - ½ (nilai minimum)

Jawaban yang tepat B.

8. Garis x = 90⁰ dan x = 270⁰ pada grafik fungsi y = tan x disebut...

a. Garis normal

b. Garis tegak lurus

c. Garis sumbu

d. Garis kontinu

e. Asimtot

Jawab:

Pada grafik fungsi y = tan x saat x = 90⁰ dan x = 270⁰ membentuk garis asimtot.

Jawaban yang tepat E.

9. Titik koordinat dari fungsi trigonometri f(x) = sin 2x pada x = -120⁰ adalah...

a. (-150⁰; ½ √3)

b. (-120⁰; ½ √3)

c. (120⁰; ½ √3)

d. (-120⁰; - ½ √3)

e. (150⁰, -½ √3)

Jawab:

f(x) = sin 2x

f(-120⁰) = sin 2 (-120⁰)

     = sin -2400

     = sin –(180⁰ + 60⁰)

      = - sin -600

     = ½ √3

Jadi, jawaban yang tepat B.

10. Grafik yang benar untuk f(x) = sin 2x adalah...

Jawab:

f(x) = sin 2x

f(0⁰) = sin 2(0⁰) = sin 0⁰ = 0 maka titiknya (0⁰, 0)

f(30⁰) = sin 2(30⁰) = sin 60⁰ = ½ √3 maka titiknya (30⁰, ½ √3)

f(90⁰) = sin 2(90⁰) = sin 180⁰ = 0 maka titiknya (90⁰, 0)

Gambar yang sesuai adalah A.

11. Perhatikan gambar berikut!

Persamaan grafik fungsi di atas adalah...

a. y = 3 cos 2x

b. y = -3 cos 2x

c. y = 3 cos ½ x

d. y = -3 cos ½ x

e. y = -3 cos 2x

Jawab:

Grafik di atas adalah grafik cosinus.

Bentuk umum fungsinya adalah y = k . cos a (x ± α)

k = -3

Maka persamaan yang memenuhi grafik di atas adalah y = -2 cos 2x

Jawaban yang tepat B.

12. Nilai minimum dari fungsi trigonometri f(x) =sin (2x + 30⁰) adalah...

a. -1

b. 0

c. 1

d. 2

e. 3

Jawab:

f(x) =sin (2x + 30⁰)

y = 1 (nilai maksimum)

y = -1 (nilai minimum)

Jawaban yang tepat A.

13. Diketahui f(x) = cos (2x - 30⁰). Nilai yang benar untuk x = 195⁰ adalah...

a. 2

b. 1

c. 0

d. -1

e. -2

Jawab:

f(x) = cos (2x - 30⁰)

f(195⁰) = cos (2(195⁰) - 30⁰)

    = cos (390⁰ – 30⁰)

    = cos 3600

    = 1

Jawaban yang tepat B.

14.diketahui persamaan trigonometri sin 2x = cos 3x,  maka himpunan penyelesaiannya adalah….

a. (18°, 60°, 162°, 234°, 306°)

b. (28°, 90°, 162°, 234°, 306°)

c. (18°, 90°, 162°, 234°, 306°)

d. (18°, 90°, 162°, 234°, 309°)

e. (18°, 90°, 162°, 243°, 306°)

Jawab:

sin 2x = cos 3x

sin 2x = sin (90° – 3x)

2x = 90° – 3x + k 360°

5x = 90° + k 360°

5x = 90° x = 18

Atau 5x = 90° + 360° x = 90

atau 5x = 90° + 720° x = 162

atau 5x = 90° + 1080° x = 234

Atau 5x = 90° + 1440° x = 306

Himpunan penyelesaian dari sin 2x = cos 3x adalah (18°, 90°, 162°, 234°, 306°).

Jawaban yang tepat C.

15.Tentukan himpunan penyelesaian dari persamaan 2 sin² 3x + 2 sin 3x = -4 !

a.18°

b.20°

c.27°

d.32°

e.30°

Jawab:

2 sin² 3x + 2 sin 3x = -4

2 sin² 3x + 2 sin 3x + 4 = 0

sin² 3x + sin 3x + 2 = 0

(sin 3x + 2)(sin 3x – 1) = 0

sin 3x + 2 sin 3x = -2 (tidak bisa)

Atau sin 3x – 1 sin 3x = 1 = sin 90 3x = 90 x  = 30

Himpunan penyelesaian dari 2 sin² 3x + 2 sin 3x = -4 adalah (30°)

Jawaban yang tepat E

16.Tentukan himpunan penyelesaian dari persamaan 3 cos x + 4 sin x = 5.

a.3°,183°

b.3°,138°

c.4°,183°

d.3°,143°

e.3°,283°

Jawab:

Rumus trigonometri

Jawaban yang tepat A

17.Perhatikan grafik fungsi berikut.

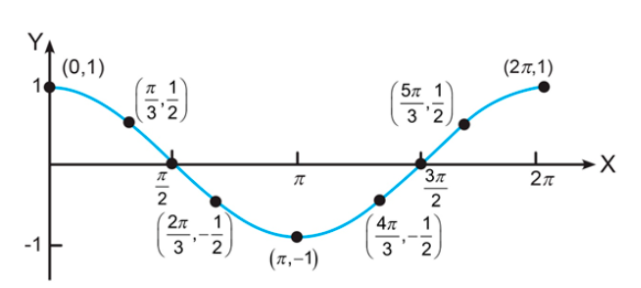
Grafik fungsi tersebut merupakan grafik fungsi jenis apa?

a. grafik fungsi y = cos x untuk 0 ≤ x ≤ 3π.

b. grafik fungsi y = cos x untuk 0 ≤ x ≤ 2π.

c. grafik fungsi y = sin x untuk 0 ≤ x ≤ 2π.

d. grafik fungsi y = tan x untuk 0 ≤ x ≤ 2π.

e. grafik fungsi y = cos x untuk 0 ≤ x ≤ 4π.

Jawab:

Jika diperhatikan, grafik tersebut dimulai dari titik (0,1) dan mempunyai periode satu putaran 0 ≤ x ≤ 2π.

Dengan demikian, grafik fungsi tersebut adalah grafik fungsi cos, yaitu y = cos x. Untuk meyakinkan, coba lihat salah satu titiknya.

Jadi, grafik fungsi tersebut merupakan grafik fungsi y = cos x untuk 0 ≤ x ≤ 2π.

Jawaban yang tepat B

18.Hitunglah nilai maksimum dan minimum fungsi y = cos (x – 30), x ∈ [0^o, 360^o].

a.(11,-1)

b.(-1,-1)

c.(1,1)

d.(1,-1)

e.(-1,1)

Jawab:

Berdasarkan tabel trigonometri untuk sudut istimewa, diperoleh:

Berdasarkan tabel di atas, nilai maksimum dari fungsi y = cos (x – 30), x ∈ [0^o, 360^o] adalah 1 dan nilai minimumnya adalah –1.Jadi=(1,-1)

Jawaban yang tepat D

19.Turunkan fungsi berikut:y = 5 sin x 

a.y' = 5,5 cos x 

b.y' = 5 cos x 

c.y' = 0,5 cos x 

d.y' = 5 tan x 

e.y' = 5 sin x 

Jawab:

y = 5 sin x

y' = 5 cos x 

Jawaban yang tepat B

20.Tentukan turunan pertama dari y=-4 sin x

a. y'=-4 sin x

b. y'=4 sin x

c. y'=-4 cos x

d. y'=-4 tan x

e. y'=-4,1sin x

Jawab:

y=-4 sin x

y'=-4 sin x

Jawaban yang tepat A

21.Diberikan y=-2 cos x. Tentukan y'

a. y'=-2 cos x

b. y'=2 cos x

c. y'=2 tan x

d. y'=-2 sin x

e. y'=2 sin x

Jawab:

y =-2 cos x

y'=-2 (-sin x) 

y'=2 sin x

Jawaban yang tepat E

22.Tentukan y' dari y = 4 sin x + 5 cos x 

a. y ' = 5 cos x − 4 sin x

b. y ' = -4 cos x − 5 sin x

c. y ' = 4 cos x − 5 sin x

d. y ' = 4 cos x + 5 sin x

e. y ' = 4 sin x − 5 tan x

Jawab:

y = 4 sin x + 5 cos x

y' = 4 (cos x) + 5 (−sin x) 

y ' = 4 cos x − 5 sin x

Jawaban yang tepat C

23.Tentukan turunan dari

y = 5 cos x − 3 sin x 

a. y' = 5 sin x − cos x

b. y' = −5 sin x − cos x

c.y' = −5 sin x + cos x

d. y' = −5 sin x − 2 cos x

e. y' = −5 sin x − 1,5 cos x

Jawab:

y = 5 cos x − 3 sin x

y' = 5 (−sin x) − 3 (cos x) 

y' = −5 sin x − cos x

Jawaban yang tepat B

24.Tentukan turunan dari:

y = sin (2x + 5) 

a. y' = 2 cos (-2x + 5)

b. y' = 2 cos (4x + 5)

c. y' = 2 cos (2x + 5)

d. y' = 2 cos (2x + 5)

e. y' = 2 cos (2x - 5)

Jawab:

Dengan aplikasi turunan berantai maka untuk

y = sin (2x + 5) 

y ' = cos (2x + 5) ⋅ 2

                            ↑

Angka 2 diperoleh dari menurunkan 2x + 5

y' = 2 cos (2x + 5)

Jawaban yang tepat D

25.Tentukan turunan dari y = cos (3x −1)

a. y' = − 3 sin (3x − 1)

b. y' =  3 sin (3x − 1)

c. y' = − 3 sin (3x + 1)

d. y' = − 3 sin (6x − 1)

e. y' = − 3 sin (3 − 1)

Jawab:

Dengan aplikasi turunan berantai maka untuk

y = cos (3x − 1) 

y ' = − sin (3x −1) ⋅ 3

                             ↑

Angka 3 diperoleh dari menurunkan 3x − 1

Hasil akhirnya adalah

y' = − 3 sin (3x − 1)

Jawaban yang tepat A

26.Tentukan turunan dari:

y = sin2 (2x −1)

a. y' = -4 sin (2x −1) cos (2x −1)

b. y' = 4 sin (2x +1) cos (2x −1)

c. y' = 4 sin (2x −1) cos (2x −1)

d. y' = 4 sin (2x −1) cos (2x +1)

e. y' = 4 sin (2x +1) cos (2x +1)

Jawab:

Turunan berantai:

y = sin2 (2x −1)

y' = 2 sin 2−1 (2x −1) ⋅ cos (2x −1) ⋅ 2

y' = 2 sin (2x −1) ⋅ cos (2x −1) ⋅ 2

y' = 4 sin (2x −1) cos (2x −1)

Jawaban yang tepat C

27.Diketahui f(x) = sin3 (3 – 2x) 

Turunan pertama fungsi f adalah f ' maka f '(x) =....

A. 6 sin2 (3 – 2x) cos (3 – 2x) 

B. 3 sin2 (3 – 2x) cos (3 – 2x) 

C. –2 sin2 (3 – 2x) cos (3 – 2x) 

D. –6 sin (3 – 2x) cos (6 – 4x) 

E. – 3 sin (3 – 2x) sin (6 – 4x) 

Jawab:

f(x) = sin3 (3 – 2x) 

Turunkan sin3 nya, 

Turunkan sin (3 – 2x) nya, 

Turunkan (3 – 2x) nya, 

Hasilnya dikalikan semua seperti ini:

f(x) = sin3 (3 – 2x) 

f ' (x) = 3 sin 2 (3 − 2x) ⋅ cos (3 − 2x) ⋅ − 2

f ' (x) = −6 sin 2 (3 − 2x) ⋅ cos (3 − 2x) 

Sampai sini sudah selesai, namun di pilihan belum terlihat, diotak-atik lagi pakai bentuk sin 2θ = 2 sin θ cos θ

f ' (x) = −6 sin 2 (3 − 2x) ⋅ cos (3 − 2x) 

f ' (x) = −3 ⋅ 2 sin (3 − 2x) ⋅ sin (3 – 2x) ⋅ cos (3 − 2x) 

f ' (x) = −3 ⋅ 2 sin (3 − 2x) ⋅ cos (3 – 2x) ⋅ sin (3 − 2x) 

                  |_______|

                                 ↓

                         sin 2 (3 − 2x)

f ' (x) = −3 sin 2(3 – 2x) ⋅ sin (3 − 2x) 

f ' (x) = −3 sin (6 – 4x) sin (3 − 2x) 

atau:

f ' (x) = −3 sin (3 − 2x) sin (6 – 4x)

Jawaban yang tepat E

28.Diketahui fungsi f(x) = sin2 (2x + 3) dan turunan dari f adalah f ′. Maka f ′(x) = … 

A. 4 sin (2x + 3) cos (2x + 3) 

B. 2 sin (2x + 3) cos (2x + 3) 

C. sin (2x + 3) cos (2x + 3) 

D. –2 sin (2x + 3) cos (2x + 3) 

E. –4 sin (2x + 3) cos (2x + 3) 

Jawab:

Turunan berantai

f(x) = sin2 (2x + 3)

Turunkan sin2 nya,

Turunkan sin (2x + 3) nya,

Turunkan (2x + 3) nya.

f '(x) = 2 sin (2x + 3) ⋅ cos (2x + 3) ⋅ 2

f '(x) = 4 sin (2x + 3) ⋅ cos (2x + 3)

DAFTAR PUSTAKA:

https://www.ajarhitung.com/2021/05/latihan-soal-fungsi-trigonometri-kelas.html

https://tambahpinter.com/fungsi-trigonometri/

https://www.quipper.com/id/blog/mapel/matematika/grafik-fungsi-trigonometri-matematika-kelas-10/

https://brainly.co.id/tugas/15696244