SUDUT-SUDUT BERELASI

 

                                          SUDUT-SUDUT BERELASI

NAMA:ARINI FITRIA AFRIZAL(03)

KELAS:X MIPA 1

Sudut Berelasi – Adalah perluasan definisi dasar ilmu trigonometri tentang kesebangunan pada segitiga siku-siku yang memenuhi untuk sudut kuadran I atau sudut lancip (0 − 90°).

Sudut-sudut yang berelasi atau berhubungan ditunjukkan dengan adanya hubungan antara sudut α dengan sudut (90° ± α), (180° ± α), (270° ± α), (360° ± α), atau -α.

Jika sudut α berelasi dengan sudut (90° - α) atau (π2 - α), maka kedua sudut dinamakan saling berpenyiku. Selanjutnya, jika sudut α berelasi dengan sudut (180° - α) atau (π - α), maka kedua sudut tersebut dinamakan saling berpelurus.

Perbandingan Trigonometri di Kuadran I

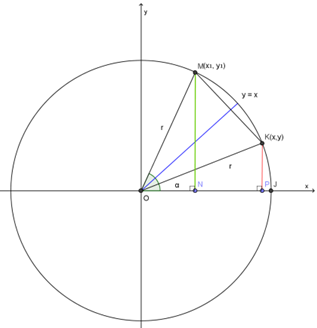
Oleh karena pada gambar di atas, titik M(x1, y1) adalah bayangan dari titik K(x, y) oleh pencerminkan terhadap garis y = x, maka

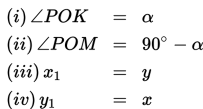
Dengan demikian, relasi antara sudut α dengan sudut (90° - α) atau (π2−α) adalah sebagai berikut:

Perbandingan Trigonometri di Kuadran II

A. Sudut α berelasi dengan sudut (180° - α) atau (π - α)

Relasi antara sudut α dengan sudut (180° - α) adalah sebagai berikut:

B. Sudut α berelasi dengan (90° + α) atau (π2 + α)

Misalkan A(x , y), OA = r, dan ∠AOC = α.

Jika α diputar dengan pusat perputaran adalah O(0,0) sejauh 90° dengan arah berlawanan arah putar jarum jam, maka bayangan titik A oleh perputaran tersebut adalah A'(-y , x).

Dengan demikian, ∠AOA' = (90° + α) dan OA = OA' = r.

Berdasarkan gambar di atas, relasi antara sudut α dengan (90° + α) adalah sebagai berikut:

Perbandingan Trigonometri di Kuadran III

A. Sudut α berelasi dengan (180° + α) atau (π + α)

Mari kita perhatikan gambar berikut.

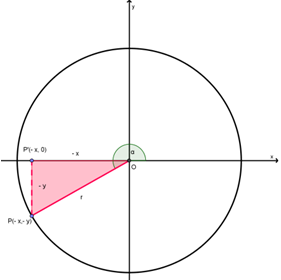
Relasi antara sudut α dengan sudut (180° + α) adalah sebagai berikut:

B. Sudut α berelasi dengan sudut (270° - α) atau (32π - α)

Misalkan A(x , y), OA = r, dan ∠AOC = α.

Jika titik A dicerminkan terhadap garis y = x, kemudian diputar dengan pusat perputaran adalah O sejauh 180° dengan arah berlawanan arah putar jarum jam, maka bayangan dari titik A adalah A"(-y, -x), dimana ∠AOA' = (270° - α) dan OA = OA" = r.

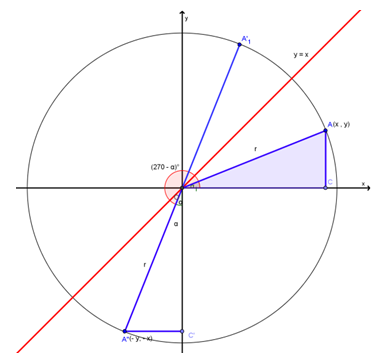
Berdasarkan gambar di atas, relasi antara sudut α dengan (270° - α) adalah sebagai berikut:

Perbandingan Trigonometri di Kuadran IV

A. Sudut α berelasi dengan (360° - α) atau (2π - α)

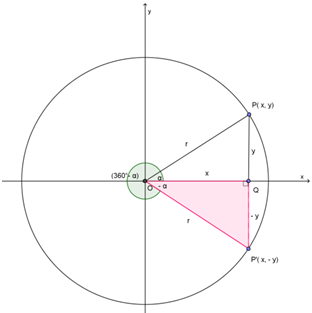
Berdasarkan gambar di atas,

• ∠QOP = α
• ∠QOP' = (360° - α)

Dengan demikian, relasi antara sudut α dengan sudut (360° - α) atau (2π - α) adalah sebagai berikut:

B. Sudut α berelasi dengan sudut (270° + α) atau (32π + α)

Jika titik A(x , y) dengan OA = r dan ∠AOB = α diputar dengan pusat O(0,0) sejauh 270° dengan arah berlawanan arah putar jarum jam, maka bayangan dari titik A adalah A'(y , x), dimana∠AOA' = (270° + α) dan OA = OA' = r.

Berdasarkan gambar di atas, relasi antara sudut α dan sudut (270° + α) adalah sebagai berikut:

C. Sudut α berelasi dengan sudut (-α)

Mari kita perhatikan gambar berikut.

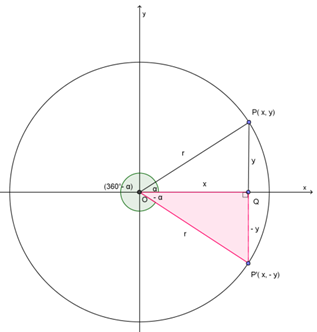
Pada gambar di atas,

• ∠QOP = α → berlawanan arah dengan arah putar jarum jam
• ∠QOP' = -α → searah dengan arah putar jarum jam

Dengan demikian,

Jika diperhatikan, rumus-rumus diatas mempunyai pola yang hampir sama, oleh karena itu sangatlah tidak bijak jika harus menghafalnya satu per satu. Ada 2 hal yang harus diperhatikan, yaitu sudut relasi yang dipaka dan tanda untuk tiap kuadran.

 

Untuk relasi (90° ± α°) atau (270° ± α°), maka :
sin → cos
cos → sin
tan → cot

 

Untuk relasi (180° ± α°) atau (360° ± α°), maka :
sin = sin
cos = cos
tan = tan

 

Tanda masing-masing kuadran :
Kuadran I (0° − 90°) = semua positif
Kuadran II (90° − 180°) = sinus positif
Kuadran III (180° − 270°) = tangen positif.
Kuadran IV (270° − 360°) = cosinus positif

Contoh 1
Untuk setiap perbandingan trigonometri berikut, nyatakan dalam perbandingan trigonometri sudut komplemennya !
sin 20°
tan 40°
cos 53°

Jawab :
sin 20° = sin (90° − 70°)
 20° = cos 70°

tan 40° = tan (90° − 50°)
tan 40° = cot 50°

cos 53° = cos (90° − 37°)
 53° = sin 37°

Jika kita perhatikan sin berubah menjadi cos, tan berubah menjadi cot dan cos berubah menjadi sin dikarenakan relasi yang digunakan adalah (90° − α) dan ketiga perbandingan trigonometri diatas bernilai positif, karena sudut 20°, 40° dan 53° berada di kuadran I.

Contoh 2
Nyatakan setiap perbandingan trigonometri berikut dalam sudut 37° !
tan 143°
sin 233°
cos 323°

Jawab :
Sudut 143° terletak pada kuadran II, sehingga tan 143° bernilai negatif.
tan 143° = tan (180° − 37°)
tan 143° = -tan 37°

Sudut 233° terletak pada kuadran III, sehingga sinus bernilai negatif.
sin 233° = sin (270° − 37°)
tan 233° = -cos 37°
Perhatikan bahwa sin berubah menjadi cos karena relasi yang digunakan (270° −  α)

Sudut 323° terletak pada kuadran IV, sehingga cosinus bernilai positif.
cos 323° = cos (360° − 37°)
 323° = cos 37°


Contoh 3
Tanpa menggunakan kalkulator, tentukan nilai dari $\frac{sin{100}^{\circ }-cos{190}^{\circ }}{cos{350}^{\circ }-sin{260}^{\circ }}$

Jawab :
sin 100° = sin (90° + 10°) = cos 10°
cos 190° = cos (180° + 10°) = -cos 10°
cos 350° = cos (360° − 10°) = cos 10°
sin 260° = sin (270° − 10°) = -cos 10°

Sehingga :
$\frac{sin{100}^{\circ }-cos{190}^{\circ }}{cos{350}^{\circ }-sin{260}^{\circ }}=\frac{cos{10}^{\circ }-(-cos{10}^{\circ })}{cos{10}^{\circ }-(-cos{10}^{\circ })}=\frac{2cos{10}^{\circ }}{2cos{10}^{\circ }}=1$


Contoh 4
Jika (x + 20°) adalah sudut lancip, tentukan nilai dari $\frac{tan(x+{110}^{\circ })}{2cot(x+{20}^{\circ })}$

Jawab :
tan (x + 110°) = tan (90° + (x + 20°))
Karena (x + 20°) lancip, maka (90° + (x + 20°)) adalah sudut kuadran II, sehingga tangen bernilai negatif.
tan (90° + (x + 20°)) = -cot (x + 20°)

akibatnya
$\frac{tan(x+{110}^{\circ })}{2cot(x+{20}^{\circ })}=\frac{-cot(x+{20}^{\circ })}{2cot(x+{20}^{\circ })}=-\frac{1}{2}$


Contoh 5
Diketahui cot (x + 36°) = tan 2x. Jika 2x adalah sudut lancip, tentukan nilai x !

Jawab :
cot (x + 36°) = tan 2x
Karena 2x sudut lancip, pastilah 2x terletak dikuadran I. Dengan menggunakan relasi sudut kuadran I, maka :
tan 2x = cot (90° − 2x)

Sehingga
cot (x + 36°) = cot (90° − 2x)
x + 36 = 90° − 2x
3x = 54
x = 18


Contoh 6
Tentukan nilai dari setiap perbandingan trigonometri berikut !

a.  cos 135°
Jawab :
Sudut 135° terletak di kuadran II, sehingga cosinus bernilai negatif.
cos 135° = cos (180 − 45°)
 135° = -cos 45°
135° = -$\frac{1}{2}$√2

b.  tan 120°
Jawab :
Sudut 120° terletak di kuadran II, sehingga tangen bernilai negatif.
tan 120° = tan (180 − 60°)
tan 120° = -tan 60°
tan 120° = -√3

c.  sin 210°
Jawab :
Sudut 210° terletak di kuadran III, sehingga sinus bernilai negatif.
sin 210° = sin (180° + 30°)
 210° = -sin 30°
 210° = -$\frac{1}{2}$

d.  tan 225°
Jawab :
Sudut 225° terletak di kuadran III, sehingga tangen bernilai positif.
tan 225° = tan (180° + 45°)
tan 225° = tan 45°
tan 225° = 1

e.  cos 315°
Jawab :
Sudut 315° terletak di kuadran IV, sehingga cosinus bernilai positif.
cos 315° = cos (360° − 45°)
15° = cos 45°
5° = $\frac{1}{2}$√2

f.  sin 300°
Jawab :
Sudut 300° terletak di kuadran IV, sehingga sinus bernilai negatif.
sin 300° = sin (360° − 60°)
00° = -sin 60°
 300° = -$\frac{1}{2}$√3

g.  sin 150° dan csc 150°
Jawab :
Sudut 150° terletak di kuadaran II, sehingga sinus bernilai positif.
sin 150° = sin (180 − 30°)
 150° = sin 30°
150° = $\frac{1}{2}$

csc 150° = $\frac{1}{sin{150}^{\circ }}$
150° = $\frac{1}{\frac{1}{2}}$
 150° = 2

h.  cos 240° dan sec 240°
Jawab :
Sudut 240° terletak di kuadran III, sehingga cosinus bernilai negatif.
cos 240° = cos (180° + 60°)
 240° = -cos 60°
240° = -$\frac{1}{2}$

sec 240° = $\frac{1}{cos{240}^{\circ }}$
240° = $\frac{1}{-\frac{1}{2}}$
240° = -2

i.  tan 330° dan cot 330°
Jawab :
Sudut 330° terletak di kuadran IV, sehingga tangen bernilai negatif.
tan 330° = tan (360° − 30°)
tan 330° = -tan 30°
tan 330° = -$\frac{1}{3}$√3

cot 330° = $\frac{1}{tan{330}^{\circ }}$
330° = $\frac{1}{-\frac{1}{3}\sqrt{3}}$
 330° = -√3



Contoh 7
Tentukan nilai dari :
sin (-30°)
cos (-135°)
tan (-330°)

Jawab :
sin (-30°) = -sin 30°
(-30°) = -$\frac{1}{2}$

cos (-135°) = cos 135°  (K.II cos negatif)
(-135°) = cos (180° − 45°)
-120°) = -cos 45°
-120°) = -$\frac{1}{2}$√2

tan (-330°) = -tan 330°  (K.IV tan negatif)
tan (-330°) = -{tan (360° − 30°)}
tan (-300°) = -{-tan 30°}
tan (-300°) = tan 30°
tan (-300°) = $\frac{1}{3}$√3

Contoh 8
Tentukan nilai dari sin 780°
Jawab :
sin 780° = sin (60° + 2. 360°)

= sin 60°

80° = $\frac{1}{2}$√3


Contoh 9
Tentukan nilai dari tan 690°
Jawab :
tan 690° = tan (330° + 1. 360°)
tan 690° = tan 330°  (K.IV tan negatif)
tan 690° = tan (360° − 30°)
tan 690° = -tan 30°
tan 690° = -$\frac{1}{3}$√3 atau

tan 690° = tan (-30° + 2. 360°)
5° = tan (-30°)
 405° = -tan 30°
405° = -$\frac{1}{3}$√3


Contoh 10
Tentukan nilai dari cos 1200°
Jawab :
cos 1200° = cos (120° + 3. 360°)
00°    = cos 120° (K.II cos negatif)
1200° = cos (180° − 60°)
1200° = -cos 60°
1= -$\frac{1}{2}$

DAFTAR PUSTAKA:

https://www.danlajanto.com/2015/10/sudut-sudut-berelasi-trigonometri-sma_58.html

https://smatika.blogspot.com/2017/04/perbandingan-trigonometri-sudut-berelasi.html

https://ufitahir.wordpress.com/2020/03/18/menentukan-nilai-sudut-berelasi-berbagai-kuadran/