SOAL PERSAMAAN DAN PERTIDAKSAMAAN RASIONAL DAN IRASIONAL
SOAL PERSAMAAN DAN PERTIDAKSAMAAN RASIONAL DAN IRASIONAL
CONTOH SOAL PERSAMAAN RASIONAL:
1.√(x-2) + x = 14, tentukan nilai x-nya?
Penyelesaian :
√(x-2) + x = 14 diubah menjadi √(x-2) = 14 - x
Syarat, agar √(x-2) nyata adalah x -2≥ 0 maka x ≥ 2 …………(1)
Mereka harus positif atau nol maka 14 – x ≥ 0, maka x ≤ 14 ……………(2)
Dari pernyataan (1) dan (2) diperoleh, sehingga syaratnya 2 ≤ x ≤ 14
Sehingga =
√(x-2) = 14 – x kedua ruas dikuadratkan :
(√(x-2) )2 = (14 – x )2
x – 2= 196 – 28x + x2
x2 – 29x + 198 = 0
( x – 11 ) ( x – 18 ) = 0
X = 11 x = 18
Sesuai syarat yang ada maka x adalah = 11
Selain syarat agar akar-akar nyata perlu diperhatikan tanda kedua ruas harus sama (positif atau negatif).
CONTOH SOAL PERTIDAKSAMAAN RASIONAL:
Pembuat nol :
x − 3 = 0 ⇒ x = 3
x + 1 = 0 ⇒ x = −1
Syarat :
x + 1 ≠ 0 ⇒ x ≠ −1
Untuk interval x < −1, ambil x = −2 :
= 5 (+)
Untuk interval −1 < x ≤ 3, ambil x = 0 :
= −3 (−)
Untuk interval x > 3, ambil x = 4 :
= (+)
Karena pertidaksamaan bertanda "≥", maka daerah penyelesaian berada pada interval yang bertanda (+).
CONTOH SOAL PERSAMAAN IRASIONAL:
Tentukan nilai x :
1. Akar 2x - 4 =
2. Akar 3x + 21 =
3. Akar X² - 3x - 10 =
Jawaban :
1. 2x - 4 > 0
= 2 x > 4
= x > 2.
2. 3x + 21 > 0
= 3x > - 21
=x > - 7.
3. X² - 3x - 10 > 0
= ( x - 5 )( x + 2 ) > 0
= x > -2 atau x > 5

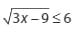
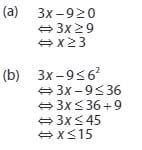

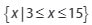


Komentar
Posting Komentar