NILAI MUTLAK
NILAI MUTLAK
Pengertian Nilai Mutlak
Semua bilangan mempunyai nilai mutlak nya masing masing. Semua bilangan mutlak bernilai positif, sehingga nilai bilangan mutlak dari bilangan dengan angka yang sama namun beda notasi positif (+) dan negatif (-) akan mempunyai hasil bilangan mutlak yang sama.
Jika x anggota dari bilangan riil, maka nilai mutlak ditulis dengan |x| dan didefinisikan sebagai berikut:
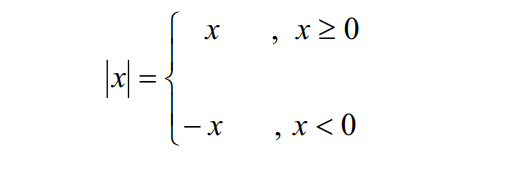
------------------------------------------------------------------Sifat-sifat Nilai Mutlak
Pada operasi persamaan bilangan mutlak, terdapat sifat-sifat bilangan mutlak yang dapat membantu menyelesaikan persamaan bilangan mutlak.
-------------------------------------------
Sifat-sifat nilai mutlak pada pertidaksamaan:
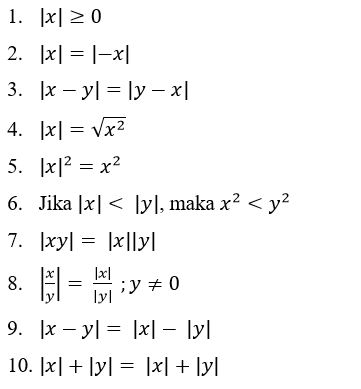
Contoh Soal 1
Berapa nilai mutlak dari persamaan |10-3|?
Jawab :
|10-3|=|7|=7
Contoh Soal 2
Berapa hasil x untuk persamaannilai mutlak |x-6|=10?
Jawab:
Untuk menyelesaikan persamaan tersebut, terdapat dua kemungkinan hasil bilangan mutlak
|x-6|=10
Solusi pertama:
x-6=10
x=16
solusi kedua:
x – 6= -10
x= -4
Jadi, jawaban untuk persamaan ini yaitu 16 atau (-4)
Contoh Soal 3
Selesaikan dan hitunglah nilai x pada persamaan berikut
–3|x – 7| + 2 = –13
Jawab:
–3|x – 7| + 2 = –13
–3|x – 7| = –13 – 2
–3|x – 7| = –15
|x – 7| = –15/ –3
|x – 7| = 5
Selesai sampai solusi diatas, maka nilai x mempunyai dua nilai
x – 7=5
x=12
atau
x – 7 = – 5
x=2
sehingga hasil akhir nilai x adalah 12 atau 2
Contoh Soal 4
Selesaikan persamaan berikut dan berapa nilai x
|7 – 2x| – 11 = 14
Jawab:
|7 – 2x| – 11 = 14
|7 – 2x| = 14 + 11
|7 – 2x| = 25
Selesai pada persamaan diatas, maka bilangan untuk nilai mutlak x adalah sebagai berikut
7 – 2x = 25
2x = – 18
x= – 9
atau
7 – 2x = – 25
2x = 32
x = 16
Sehingga hasil akhir nilai x adalah (– 9) atau 16
Contoh Soal 5
Tentukan penyelesaian dari persamaan nilaimutlak berikut:
|4x – 2| = |x + 7|
Jawab:
Untuk menyelesaikan persamaan diatas, menggunakan dua kemungkinan peyelesaian yaitu:
4x – 2 = x + 7
x = 3
atau
4x – 2 = – ( x + 7)
x= – 1
Jadi penyelesian persamaan |4x – 2| = |x + 7| adalah x = 3 atau x= – 1
Contoh Soal 6
Tentukan penyelesaian persamaan nilaimutlak berikut:
|3x+2|²+|3x+2| – 2=0
Berapa nilai x?
Jawab:
Penyederhanaan : |3x+2| = p
maka
|3x+2|²+|3x+2|-2=0
p² + p – 2 = 0
(p+2) (p – 1) = 0
p+2 = 0
p = – 2 (nilai mmutlak tidak negatif )
atau
p – 1 = 0
p = 1
|3x+2| = 1
Sampai pada penyelesaian diatas, maka terdapat 2 kemungkinan jawaban untuk x, yaitu:
3x+2 = 1
3x = 1 – 2
3x = – 1
x = – 1/3
atau
– (3x+2) = 1
3x+2 = – 1
3x = – 1 – 2
3x = – 3
x = – 1
Jadi penyelesaian persamaan tersebut adalah x= – 1/3 atau x= – 1
------------------------------------------------------------------
Sifat-sifat nilai mutlak pada pertidaksamaan:
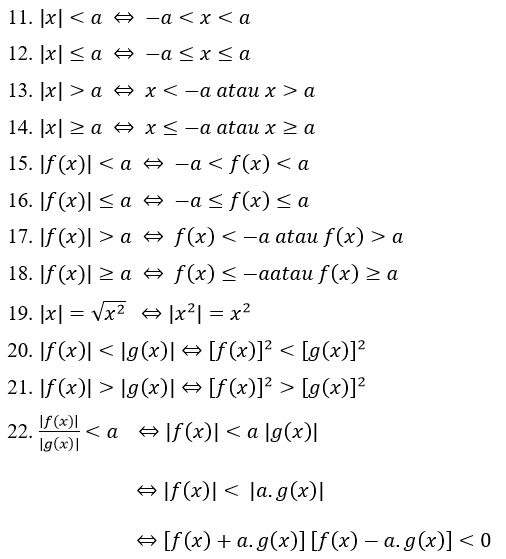
Contoh Soal 1
Carilah himpunan penyelesaian dari pertidaksamaan | x + 1 | < 3 adalah . . .
Jawaban :
Contoh Soal 2
Selesaikanlah dari pertidaksamaan | x + 3 | < 2 – x adalah . . .
Jawaban :
Contoh Soal 3
Selesaikanlah | 3x + 7|> | 4x -8 | adalah. . .
Jawaban :
Contoh Soal 4
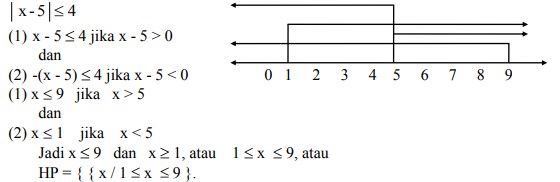
Carilah himpunan penyelesaian dari pertidaksamaan harga mutlak | x – 5 | ≤ 4 adalah . . .
Jawaban :
Menurut definisi harga mutlak
Contoh Soal 5
Carilah himpunan penyelesaian | x² – 10 | < 6
Jawaban :
Cara Pertama :
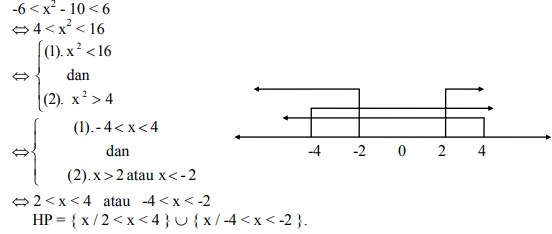
Cara kedua :
Contoh Soal 6
Buktikanlah, bahwa untuk setiap x, y, z ∈ R berlaku | x – y| ≤ | x – z | + | z – y | adalah. . .
Jawaban :
Contoh Soal 7
Selesaikanlah pertidaksamaan | 3x + 2| > 5 adalah. . .
Jawaban :
Contoh Soal 8
Selesaikanlah pertidaksamaan | 3x + 2| > | 3x + 2| adalah. . .
Jawaban :
| 3x + 2| > | 3x + 2|
Contoh Soal 9
Tentukan penyelesaianya dan lukiskan garis bilangannya dari 10 – 5x < 2x – 11 adalah. . .
Jawaban :
Contoh Soal 10
Selesaikan pertidaksamaan berikut :
| 2x – 1 |≤ 9
Jawaban :
Berdasarkan definisi nilai mutlak, diperoleh
| 2x – 1 |≤ 9
daftar pustaka:

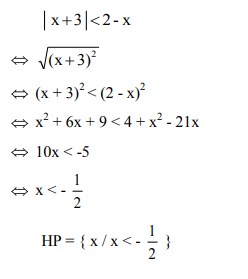

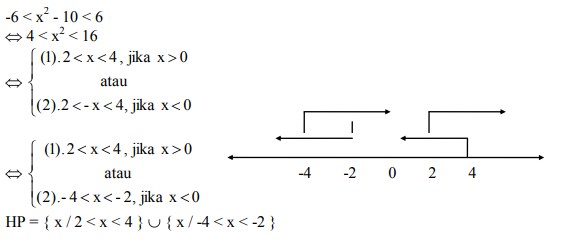







Komentar
Posting Komentar