SOAL KOMPOSISI FUNGSI DAN INVERS FUNGSI
CONTOH SOAL KOMPOSISI FUNGSI DAN INVERS FUNGSI
Contoh Soal Fungsi Komposisi
1. Jika f(x) = 3x + 2 dan g(x) = 4x2 . Maka (f o g)(x) dan (g o f)(x) adalah …
a.(f o g)(x) = 12x2 + 3 dan (g o f)(x) = 36x2 + 48x + 6.
b.(f o g)(x) = 12x2 + 2 dan (g o f)(x) = 36x2 + 48x + 16.
c.(f o g)(x) = 12x2 + 4 dan (g o f)(x) = 36x2 + 48x + 19.
d.(f o g)(x) = 14x2 + 2 dan (g o f)(x) = 36x2 + 48x + 26.
e.(f o g)(x) = 12x2 + 2 dan (g o f)(x) = 46x2 + 48x + 16.
Jawaban : B
(f o g)(x) = f (g(x))
(f o g)(x) = f (4x2)
(f o g)(x) = 3(4x2) + 2
(f o g)(x) = 12x2 + 2
(g o f)(x) = g(f(x))
(g o f)(x) = 4(3x + 2)2
(g o f)(x) = 4(9x2 + 12x + 4)
(g o f)(x) = 36x2 + 48x + 16
Jadi, (f o g)(x) = 12x2 + 2 dan (g o f)(x) = 36x2 + 48x + 16.
2. Diketahui (f o g)(x) = 2x + 4 dan f(x) =x – 2. Tentukan fungsi g (x)!
a.fungsi g(x)+2x+9
b.fungsi g(x)+4x+6
c.fungsi g(x)+2x+6
d.fungsi g(x)-2x+9
e.fungsi g(x)-4x+6
Jawaban : C
(f o g)(x) = 2x + 4
f(g(x)) = 2x + 4
g(x) – 2 = 2x + 4
g(x) = 2x + 4 + 2
g(x) = 2x + 6
jadi,fungsi g(x)+2x+6
3. Jika f(x) = 2x² + 5x dan g(x) = 1/x maka (fog) (2) adalah …
a.3
b.2
c.1
d.½
e.1/3
Jawaban : A
-----------------------------------------------------------------------------------------------------------------------------
4. Diketahui fungsi 𝑓(𝑥) = 2𝑥 + 1 dan 𝑔(𝑥) = 𝑥² − 3𝑥 + 3. Jika nilai (𝑔 o f) (𝑡) = 7 maka nilai t adalah …
a. 1 atau 2
b. -2/3 atau 1
c. -1 atau 2/3
d. -1 atau 3/2
e. -2 atau -1
Jawaban : D
Jawaban : A
untuk fungsi (g o f o h)(x) = ( g( f( h(x))) sehingga dapat dipermudah dengan mencari f(h(x)) terlebih dahulu
(f o h)(x) = f(h(x)) ->sisipkan fungsi h(x) ke f(x)
= f(2x - 1) ->subtitusi h(x) ke f(x)
= 3(2x - 1) + 7 ->hitung hasilnya
= 6x - 3 + 7
= 6x + 4
Jadi nilai(f o h)(x) = 6x + 4
Setelah itu kita subtitusikan f(h(x)) ke g(x) atau ( g( f( h(x))
(g o f o h)(x) = ( g( f( h(x))) ->sisipkan fungsi f(h(x)) ke g(x)
= g(6x + 4) ->subtitusi f(h(x)) ke g(x)
= 1(6x + 4) - 3 ->hitung hasilnya
= 6x + 4 - 3
= 6x + 1
Jadi nilai (g o f o h)(x) = 6x + 1
--------------------------------------------------------------------------------------------------
6.Diketahui: Dua buah fungsi f(x) = 3x - 2 dan g(x) = 2x2 + 3. Tentukan nilai fungsi komposisi(f o g)(-1)!
a.(f o g)(-1) = 23
b.(f o g)(-1) = 33
c.(f o g)(-1) = 43
d.(f o g)(-1) = 13
e.(f o g)(-1) = 53
Jawaban : D
(f o g)(x) = f(g(x)) ->sisipkan fungsi g(x) ke f(x)
= f(2x2 + 3) ->subtitusi g(x) f(x)
= 3(2x2 + 3) - 2 ->hitung hasilnya
= 6x2 + 9 - 2
(f o g)(x) = 6x2 + 7
Tentukan nilai (f o g)(-1)!
(f o g)(-1) = 6x2 + 7 ->subtitusi -1 ke (f o g)(x)
= 6(-1)2 + 7
= 6(1) + 7
= 13
Jadi nilai (f o g)(-1) = 13
--------------------------------------------------------------------------------------------------
Contoh Soal Fungsi Invers
1.Diketahui f(x) = x + 2 dan g(x) = x2 – 4. Tentukan (f + g)(x).
a.(f + g)(x)= x2 + x – 2
b.(f + g)(x)= 2x2 + x – 2
c.(f + g)(x)= x2 + x + 2
d.(f + g)(x)= x2 + 2x – 2
Jawab:A
(f + g)(x) = f(x) + gx)
(f + g)(x)= x + 2 + x2 – 4
(f + g)(x)= x2 + x – 2
-----------------------------------------------------------------------------------------------------------------------------
2.Diketahui f(x) = x2 – 3x dan g(x) = 2x + 1. Tentukan (f – g)(x).
a.(f – g)(x)= x2 – 4x – 1
b.(f – g)(x)= x2 – 5x – 1
c.(f – g)(x)= x2 + 5x – 1
d.(f – g)(x)= x2 – 5x + 1
Jawab:B
(f – g)(x) = f(x) – g(x)
(f – g)(x)= x2 – 3x – (2x + 1)
(f – g)(x)= x2 – 3x – 2x – 1
(f – g)(x)= x2 – 5x – 1
-----------------------------------------------------------------------------------------------------------------------------
3.Diketahui f(x) = x – 5 dan g(x) = x2 + x. Tentukan (f × g)(x).
a.(f × g)(x)= x3 + 4x2 – 3x
b.(f × g)(x)= x3 – 6x2 + 5x
c.(f × g)(x)= x3 – 4x2 – 5x
d.(f × g)(x)= 23 + 4x2 – 4x
Jawab:C
(f × g)(x) = f(x) . g(x)
(f × g)(x)= (x – 5)(x2 + x)
(f × g)(x)= x3 + x2 – 5x2 – 5x
(f × g)(x)= x3 – 4x2 – 5x
-----------------------------------------------------------------------------------------------------------------------------
4.Diketahui f(x) = -(2-3x) /2 , maka f-¹(x) sama dengan....
b. ⅔ (1 - x)
c. 3/2 (1 + x)
d. -⅔ (1 + x)
e. -3/2 (x - 1)
f(x) = -(2-3x) /2
f(x) = (-2+3x) /2
y = (-2+3x) /2
2y = -2+3x
2y + 2 = 3x
x = (2y+2) /3
f-¹(x) = (2x+2) /3
f-¹(x) = 2(x+1) /3
f-¹(x) = ⅔ (x + 1)
5.Diketahui . Maka
Jawab:
Sederhanakan dahulu bentuknya :
Setelah bentuknya sederhana, gunakan rumus cepat fungsi invers pecahan.
Maka diperoleh :
-----------------------------------------------------------------------------------------------------------------------------
6.Diketahui . Maka
Jawab:
gunakan rumus cepat fungsi invers pecahan :
atau bisa juga menggunakan rumus biasa :
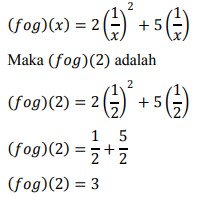
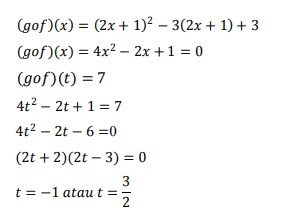


Komentar
Posting Komentar