KOMPOSISI FUNGSI DAN INVERS FUNGSI
KOMPOSISI FUNGSI
Fungsi komposisi merupakan suatu penggabungan operasi pada dua jenis fungsi f (x) dan g (x) sampai menghasilkan fungsi baru. Operasi fungsi komposisi biasa yaitu dilambangkan dengan “o” dan dibaca dengan komposisi atau bundaran.
Misalkan fungsi
f :A→B ditentukan dengan rumus y=fx
g :B→C ditentukan dengan rumus y=gx
Fungsi komposisi dan ditentukan dengan aturan:
h(x)=(g∘f)(x)=g(f(x))
Hal ini dapat diperjelas dengan gambar berikut.

Syarat fungsi g dan f dapat dikomposisikan (g∘f) atau (f∘g) ada, jika daerah hasil dari f adalah himpunan bagian dari daerah asal dari g, yaitu f(A)⊆Dg.
Sifat-sifat Fungsi Komposisi adalah sebagai berikut.
a. Pada umumnya, komposisi fungsi tidak bersifat komutatif.
(f∘g) (x) ≠ (g∘f)(x)
b. Komposisi fungsi bersifat assosiatif
Untuk sebarang fungsi f(x), g(x), dan h(x) berlaku sifat assosiatif.
(f∘(g∘h))(x)=((f∘g)∘h)(x)
c. Dalam komposisi fungsi terdapat unsur identitas, yaitu fungsi identitas I(x)=(x) yang memiliki sifat
(f∘I)(x)=(I∘f)(x)=f(x)
contoh soal
Diketahui f(x) = 2x + 1 dan g(x) = 3x2 . Tentukan:
a.(f o g)(x) b.(g o f)(x)
Penyelesaian:
a.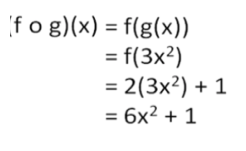
b.
Dari soal tersebut juga terlihat bahwa (f o g) (x) ≠ (g o f)(x).
*INVERS FUNGSI
Invers memiliki arti “kebalikan” jadi fungsi invers artinya fungsi kebalikan.
Fungsi invers atau fungsi kebalikan merupakan suatu fungsi yang berkebalikan dari fungsi asalnya. Suatu fungsi f memiliki fungsi invers (kebalikan) f-1 jika f merupakan fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut dapat dinyatakan sebagai berikut:
(f-1)-1 = f
Sederhananya, fungsi bijektif terjadi ketika jumlah anggota domain sama dengan jumlah anggota kodomain. Tidak ada dua atau lebih doamain berbeda dipetakan ke kodomain yang sama dan setiap kodomain memiliki pasangan di domain, perhatikan gambar di bawah ini:



Berdasarkan gambar pemetaan di atas, pemetaan pertama merupakan fungsi bijektif. Pemetaan kedua bukan fungsi bijektif karena pemetaan tersebut hanya terjadi fungsi pada. Domain d dan e dipetakan ke anggota kodomain yang sama. Pemetaan ketiga bukan fungsi bijektif karena pemetaan tersebut hanya terjadi fungsi satu-satu. Kodomain 9 tidak memiliki pasangan pada anggota domain.
Misalkan f fungsi yang memetakan x ke y, sehingga dapat ditulis y = f(x), maka f-1 adalah fungsi yang memetakan y ke x, ditulis x = f-1(y). Sebagai contoh f : A →B fungsi bijektif. Invers fungsi f adalah fungsi yang mengawankan setiap elemen B dengan tepat satu elemen pada A. Invers fungsi f dinyatakan dengan f-1 seperti di bawah ini:

Ada 3 langkah untuk menentukan fungsi invers, yaitu:
1. Ubahlah bentuk y = f(x) menjadi bentuk x = f(y).
2. Tuliskan x sebagai f-1(y) sehingga f-1(y) = f(y).
3. Ubahlah variabel y dengan x sehingga diperoleh rumus fungsi invers f-1(x).
Dalam fungsi invers terdapat rumus khusus seperti berikut:

contoh soal
Diketahui , tentukan
.
Pembahasan
Maka,
DAFTAR PUSTAKA
https://blog.teman-belajar.com/fungsi-invers-dan-fungsi-komposisi/
https://www.ruangguru.com/blog/apakah-fungsi-invers-itu
https://www.quipper.com/id/blog/mapel/matematika/fungsi-komposisi-kelas-10/
https://www.studiobelajar.com/relasi-fungsi-komposisi-invers/


Komentar
Posting Komentar