FUNGSI: KUADRAT, RASIONAL, IRASIONAL
FUNGSI: KUADRAT, RASIONAL, IRASIONAL
Fungsi Kuadrat
Bentuk umum dari fungsi kuadrat
f(x) = ax2+bx+c, dengan keterangan sebagai berikut.
Keterangan:
a = koefisien dari x2, di mana a ![]() 0
0
b = koefisien dari x
c = konstanta
Merumuskan Fungsi Kuadrat Berdasarkan Grafik
Dari grafik,diketahui titik puncak/titik balik dari suatu fungsi kuadrat, yaitu di titik (2, 1). Selain itu, diketahui juga 1 titik sembarang yaitu (1, 2). Coba rumuskan fungsi kuadratnya!
Jawaban:
Diketahui dari soal bahwa:
- (xp, yp) = (2, 1)
- Titik sembarang = (1, 2)
jika pada grafik diketahui titik puncak (xp, yp) dan 1 titik sembarang, maka gunakan rumus:
y = a(x - xp)2 + yp
2 = a(1 - 2)2 + 1
2 = a(-1)2 + 1
2 = a(1) + 1
2 = a + 1
a = 2 - 1
a = 1
Karena titik puncaknya di (2, 1) dan nilai a = 1, maka fungsi kuadratnya:
y = a(x - xp)2 + yp
y = 1(x - 2)2 + 1
y = x2 - 4x + 4 + 1
y = x2 - 4x + 5
Jadi, dari grafik tersebut fungsi kuadratnya adalah f(x) = x2 - 4x + 5Fungsi Rasional
Fungsi rasional adalah fungsi yang memetakan suatu bilangan real x ke bilangan rasional . dengan
dan
adalah polinom-polinom dan h(x) tidak sama dengan nol.
Fungsi rasional yang paling sederhana adalah fungsi y = 1/x dan fungsi y = 1/x², yang keduanya memiliki pembilang konstanta dan penyebut polinomial dengan satu suku, serta kedua fungsi tersebut memiliki domain semua bilangan real kecuali x ≠ 0.
Fungsi y = 1/x
Fungsi ini disebut juga sebagai fungsi kebalikan karena setiap kita mengambil sembarang x (kecuali nol) maka akan menghasilkan kebalikannya sebagai nilai dari fungsi tersebut.
x yang besar akan menghasilkan nilai fungsi yang kecil, demikian pula sebaliknya. Tabel dan grafik dari fungsi tersebut dapat dilihat seperti di bawah ini.

Fungsi y = 1/x²
grafik dari fungsi ini akan jeda ketika x = 0. Akan tetapi karena kuadrat dari sembarang bilangan negatif adalah bilangan positif, cabang-cabang dari grafik fungsi ini akan berada di atas sumbu-x. Perhatikan bahwa fungsi y = 1/x² merupakan fungsi genap.
 Serupa dengan y = 1/x, nilai x yang mendekati positif tak hingga, menghasilkan y yang mendekati nol: x → ∞, y → 0. Hal ini merupakan salah satu indikasi dari sifat asimtot dalam arah horizontal, dan kita mengatakan y = 0 merupakan asimtot horizontal dari fungsi y = 1/x dan y = 1/x².
Serupa dengan y = 1/x, nilai x yang mendekati positif tak hingga, menghasilkan y yang mendekati nol: x → ∞, y → 0. Hal ini merupakan salah satu indikasi dari sifat asimtot dalam arah horizontal, dan kita mengatakan y = 0 merupakan asimtot horizontal dari fungsi y = 1/x dan y = 1/x².
a. Asimtot Horizontal
Diberikan suatu konstanta k, garis y = k merupakan asimtot horizontal dari fungsi V(x) jika x bertambah tanpa batas, menyebabkan V(x) mendekati k: x → –∞, V(x) → k atau x → ∞, V(x) → k
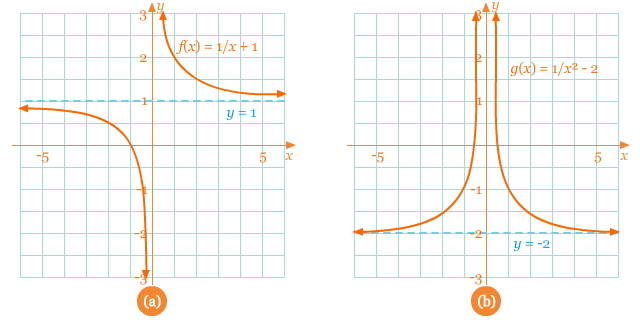
Pada gambar (a) di bawah ini menunjukkan garis asimtot horizontal pada y = 1, yang menggambarkan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan. Gambar (b) menunjukkan garis asimtot horizontal pada y = –2, yang menggambarkan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.
Contoh:
Berdasarkan gambar (b) di atas, gunakan notasi matematika untuk,
- Mendeskripsikan sifat dari ujung grafik tersebut.
- Mendeskripsikan apa yang terjadi ketika x mendekati nol.
Pembahasan
- Ketika x → –∞, g(x) → –2. Ketika x → ∞, y → –2.
- Ketika x → 0–, g(x) → ∞. Ketika x → 0+, y → ∞.
Dari contoh 2b di atas, kita dapat melihat bahwa ketika x mendekati nol, g menjadi sangat besar dan semakin bertambah tak terbatas. Hal ini merupakan indikasi dari sifat asimtot dalam arah vertikal, dan selanjutnya kita menyebut garis x = 0 merupakan asimtot vertikal untuk g (x = 0 juga merupakan asimtot vertikal untuk f)
b. Asimtot Vertikal
Diberikan suatu konstanta h, garis x = h merupakan asimtot vertikal untuk fungsi V jika x mendekati h, V(x) akan bertambah atau berkurang tanpa batas: ketika x → h+, V(x) → ±∞ atau ketika x → h–, V(x) → ±∞.
Mengidentifikasi dari asimtot horizontal dan vertikal sangatlah berguna karena grafik y = 1/x dan y = 1/x² dapat ditransformasi dengan menggesernya ke arah vertikal ataupun gorizontal. Fungsi,
merupakan bentuk pergeseran dari fungsi y = 1/x. Sedangkan fungsi,
merupakan bentuk pergeseran dari fungsi y = 1/x².
Fungsi Irasional
Fungsi irasional adalah fungsi yang memetakan himpunan bilangan real tak negatif kepada himpunan itu sendiri. Sehingga fungsi irasional memiliki syarat bahwa fungsi akan terdefinisi apabila nilai di dalam akar tersebut tidak negatif.
Contoh Soal
Suatu fungsi irasional ditentukan oleh rumus . Fungsi tersebut akan terdefinisi jika ...
Jawaban:
Pada fungsi tersebut terlihat bahwa fungsi tersebut irrasional yang di dalam akar memiliki bentuk pecahan biasa, sehingga dalam pecahan biasa memiliki syarat penyebut tidak boleh bernilai .
Dengan demikian, agar fungsi terdefinisi, maka nilai haruslah .
Daftar Pustaka
https://www.ruangguru.com/blog/matematika-kelas-10-membuat-fungsi-kuadrat-dari-grafik
https://yos3prens.wordpress.com/2014/07/28/fungsi-rasional-dan-asimtot/
https://roboguru.ruangguru.com/question/suatu-fungsi-irrasional-ditentukan-oleh-rumus-fungsi-tersebut-akan-terdefinisi-jika-_QU-8V399V7J



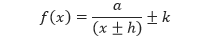
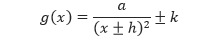


Komentar
Posting Komentar